Trees, Graphs, and Epigraphs

On the surface, the structures encoded in PENMAN Notation (see here) are a tree, and only by resolving repeated node identifiers (variables) as reentrancies does the actual graph become accessible. The Penman library thus accommodates the three stages of a structure: the linear PENMAN string, the surface tree, and the pure graph. Going from a string to a tree is called parsing, and from a tree to a graph is interpretation, while the whole process (string to graph) is called decoding. Going from a graph to a tree is called configuration, and from a tree to a string is formatting, while the whole process is called encoding. These processes are illustrated by the following figure (concepts are not shown on the tree and graph for simplicity):

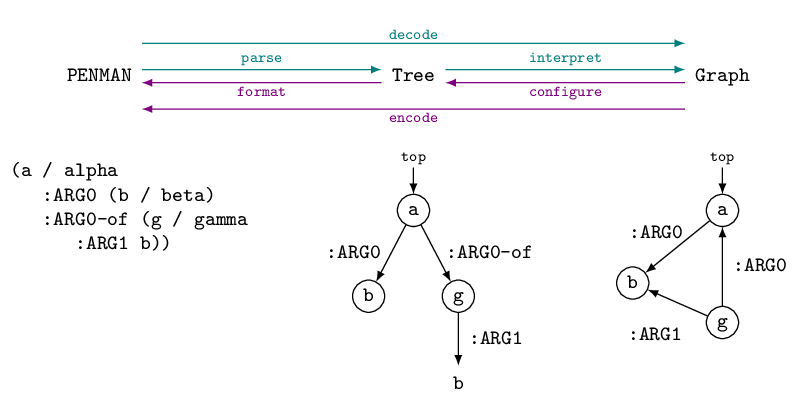
Conversion from a PENMAN string to a Tree, and vice versa, is straightforward and lossless. Conversion to a Graph, however, is potentially lossy as the same graph can be represented by different trees. For example, the graph in the figure above could be serialized to any of these PENMAN strings:

(a / alpha                (a / alpha                     (a / alpha
   :ARG0 (b / beta)          :ARG0 (b / beta                :ARG0 (b / beta
   :ARG0-of (g / gamma          :ARG1-of (g / gamma))          :ARG1-of (g / gamma
      :ARG1 b))              :ARG0-of g)                          :ARG0 a)))

Even more serializations are possible if you do not require the first occurrence of a variable to define the node (with its node label (concept) and outgoing edges), or if you allow other nodes to be the top.

The Penman library therefore introduces the concept of the epigraph (not to be confused with other senses of epigraph, such as an inscription on a building or a passage at the beginning of a book), which is information on top of the graph that instructs the codec how the graph should be serialized. The epigraph is thus analagous to the idea of the epigenome: epigenetic markers controls how genes are expressed in an individual as the epigraphical markers control how graph triples are expressed in a tree or string. Separating the graph and the epigraph thus allow the graph to be a pure representation of the triples expressed in a PENMAN serialization without losing information about the surface form.

There are currently two kinds of epigraphical markers: layout markers and surface alignment markers. Surface alignment markers are parsed from the string and stored in the tree then propagated to the graph upon interpretation. Layout markers are created when the tree is interpreted into a graph. When an edge goes to a new node and not a constant or variable, a Push marker is inserted. When a node ends, a POP marker is inserted. With these markers, and the ordering of triples, the graph can be configured to a specific tree structure.